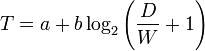Еще одним из важных уроков, который мы можем извлечь из закона Фиттса является, что несмотря на то, что легче всего щёлкнуть по самой большой кнопке, это не обязательно будет самая важная кнопка. Именно из-за этого заблуждения во множестве интерфейсов пользователей кнопки подтверждения просто огромные.

Пройти интерактивный тест:
http://fww.few.vu.nl/hci/interactive/fitts/

Математическая модель

Математически закон записывается как

где:

• — среднее время, затрачиваемое на совершение действия
• — среднее время запуска/остановки движения
• — величина, зависящая от типичной скорости движения
• — дистанция от точки старта до центра цели
• — ширина цели, измеренная вдоль оси движения

Закон Хика

Закон Фиттса обычно сопровождается законом Хика. Закон Хика - утверждение, что время реакции при выборе из некоторого числа альтернативных сигналов зависит от их числа. Словами логики - чем больше пунктов в выборе, тем дольше люди будут думать что выбрать. Поэтому везде слышны рекомендации делать не больше 5-7 пунктов в меню, использовать группировки, выделения и т. п.

Перед тем как переместить курсор к цели или совершить любое другое действие из набора множества вариантов, пользователь должен выбрать этот объект или действие. В законе Хика утверждается, что когда необходимо сделать выбор из n вариантов, время на выбор одного из них будет пропорционально логарифму по основанию 2 от числа вариантов плюс 1, при условии, что все варианты являются равновероятными. В этом виде закон Хика очень похож на закон Фитса.

Математическая модель

Время (мс) = a + b \log_2(n+1)

Если вероятность 1-го варианта равна p(i), то вместо логарифмического коэффициента используется

\sum_i p(i) \log_2(1/p(i)+1)

Коэффициенты, используемые в выражении закона Хика, в большой степени зависят от многих условий, включая то, как представлены возможные варианты, и то, насколько хорошо пользователь знаком с системой. (Если варианты представлены непонятным образом, значения a и b возрастают. Наличие навыков и привычек в использовании системы снижает значение b.) Мы не будем рассматривать эти зависимости – для нас важно, что для принятия того или иного решения требуется время; что для принятия сложных решений требуется больше времени, чем для принятия простых решений; и что взаимосвязь является логарифмической. При отсутствии более точных данных для проведения быстрых и приблизительных вычислений мы можем воспользоваться теми же значениями a и b, которые использовали для закона Фитса.

При использовании любых положительных и ненулевых значений a и b из закона Хика следует, что предоставление пользователю сразу нескольких вариантов одновременно обычно является более эффективным, чем организация тех же вариантов в иерархические группы. Выбор из одного меню, состоящего из 8 элементов, производится быстрее, чем из двух меню, состоящих их 4 элементов каждое. Если все элементы могут быть выбраны с равной вероятностью и если не учитывать время, необходимое для открытия второго меню (которое, конечно, еще более увеличило бы время для интерфейса, состоящего из двух меню), то сравнение времени для выбора одного элемента из восьми (a + b \log_2 8) с удвоенным временем для выбора одного элемента из четырех 2 (a + b \log_2 4) покажет, что

а + 3b < 2(а + 2b)

поскольку \log_2 8 = 3, a \log_2 4 = 2, а также поскольку a < 2a и 3b < 4b.

Это согласуется с данными, полученными в экспериментах со структурами меню (см. например, Norman и Chin, 1988).

Наше рассмотрение законов Фитса и Хика нельзя считать полным. Например, следует обратить внимание на то, что эти законы не случайно принимают ту же форму, что и теорема Шэннона – Хартли (Shannon-Hartley). Тем не менее, этого короткого рассмотрения вполне достаточно для того, чтобы отметить их ценность с точки зрения разработки интерфейсов. Они могут быть полезными даже в том случае, когда эмпирические значения коэффициентов a и b не известны (как это было в нашем примере). (Более подробные сведения см. в Card, Moran и Newell, 1983, с. 72–74.)